1.4 Work of adhesion and cohesion
If two phases (α and β) in contact are pulled apart inside a third phase ω, the original interface is destroyed and two new interfaces are formed (see Figure as shown below).
.png)
The work energy per unit area in performing this operation is called the work of adhesion, Wαβ. There is a contribution from each interface removed from or added to the system:
Wαβ = −γ αβ + γ αω + γ βω. (1.10)
If, instead of two distinct phases, a column of a single liquid is pulled apart, the work of cohesion is:
Wαα = 2γ αω (1.11)
as γ αα≡ 0.
When one of the phases is a solid, the expression for work of adhesion (Eq. 1.10) can be combined with the equation for the contact angle (Eq. 1.2). Dupré, in 1869, combined them to give the Young–Dupré equation:
WLS = γ VL + γ VS − γ LS = γ VL(1 + cosθ). (1.12)
Equation (1.12) shows that contact angle is a thermodynamic quantity, which can be related to the work of adhesion and interfacial free energy terms. Its significance is that it relates the work of adhesion to the readily measured quantities, γVL and θ, rather than to the inaccessible interfacial tensions involving the solid surface. When θ values are small, the work of adhesion is high and considerable energy must be spent to separate the solid from the liquid. If θ= 0°, then Wa SL = 2γLV; if θ= 90°, then WaSL = γLV, and if θ= 180°, then Wa SL = 0, which means that no work needs to be done to separate a completely spherical mercury drop from a solid surface (or a water drop from a super-hydrophobic polymer surface), and indeed these drops roll down very easily even with a 1° inclination angle of the flat substrate.
We note that in Eq. 1.10, 1.11, and 1.12 the definition of work (and symbol W) is different from that usually used as it is work per unit area (Everett, 1972, p. 597). The units are therefore J /m2 (= N /m) compared with J.
1.5 Young-Laplace equation
We will choose to think of γ in terms of energy per unit area. In the absence of gravitational or other fields, a soap bubble is spherical, as this is the shape of minimum surface area for an enclosed volume. A soap bubble of radius r has a total surface free energy of 4πr2γ and, if the radius were to decrease by d r, then the change in surface free energy would be 8πrγd r. Since shrinking decreases the surface energy, the tendency to do so must be balanced by a pressure difference across the film ΔP such that the work against this pressure difference ΔP 4πr2dr is just equal to the decrease in surface free energy. Thus:
ΔP 4πr2dr =8πrγd r (1.13)
Or
.png)
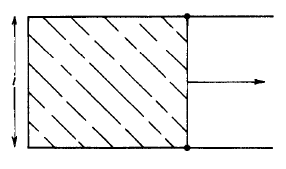
Fig. 1.8 A soap film stretched across a wire frame with one movable side.
Equation 1.10 is a special case of a more general relationship that is the basic equation of capillarity and was given in 1805 by Young and by Laplace. In general, it is necessary to invoke two radii of curvature to describe a curved surface; these are equal for a sphere, but not necessarily otherwise. A small section of an arbitrarily curved surface is shown in Fig.1-9. The two radii of curvature, RI and R2, are indicated in the figure, and the section of surface taken is small enough so that RI and R2 are essentially constant. Now if the surface is displaced a small distance outward, the change in area will be
ΔΑ=(x+dx)(y+dy)-xy=xdy+ydx (1.15)
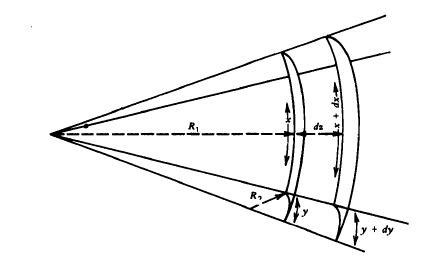
Fig.1.9 Condition for mechanical equilibrium for an arbitrarily curved surface.
The work done in forming this additional amount of surface is then
Work= γ(xdy+ydx) (1.16)
There will be a pressure difference ΔP across the surface; It acts on the area xy and through a distance dz. The corresponding work is thus
Work=ΔPxydz (1.17)
From a comparison of similar triangles, it follows that
![]() or
or ![]() (1.18)
(1.18)
And
![]() or
or ![]() (1.19)
(1.19)
If the surface is to be in mechanical equilibrium, the two work terms as given must be equal, and on equating them and substituting in the expressions for dx and dy, the final result obtained is
![]() (1.20)
(1.20)
Equation 11-7 is the fundamental equation of capillarity and is well known as Young-Laplace equation. [9]
It is apparent that Eq. 1.20 reduces to Eq. 1.14 for the case of both radii being equal, as is true for a sphere. For a plane surface, the two radii are each infinite and ΔP is therefore zero; Thus there is no pressure difference across a plane surface.
Hot keywords of USA KINO:contact angle, contact angle measurement, contact angle meter, contact angle goniometer, surface tensiometer, interfacial tensiometer, surface tension measurement, surface tension, surface tensiometry, contact angle measurement equipment and device, calculating surfac free energy, Determining Critical Micelle Concentration (CMC) of surfactant, made in China Method for choosing surface tensiometer NEW Method for choosing contact angle meter (goniometer) NEW Method for choosing interfacial tension meter NEW

Manage technical support: www.chem17.com GoogleSitemap
MainPro : contact angle,contact angle meter,contact angle goniometer,surface tension,surface tensiometer