4.1 Wetting behavior analysis and wetting envelopes
It may be imagined that up until now we have a rule which tells us if wetting will occur when placing a liquid on a solid. This comes from knowing the surface tension of the liquid and the surface energy of the solid. Thus the rule which has been formulated states that ‘a liquid, having a lower surface tension than the solid surface energy, will wet that solid’. In practice it is found that this is not always the case and it is not, therefore, an immutable rule
A2D map of wetting can be constructed by using the components of surface tension and a plot produced which is designed to show where wetting will occur. To illustrate this Owens–Wendt model described previously has been used to construct a plot.
It is suggested above that there are other ways of understanding how contact angles, hence degrees of wetting, arise from an understanding of the forces existing in the materials and between the materials. Rather than considering surface tension (or surface energy) as a single component it can be seen that surface tension is the sum of individual components, dispersive and polar components for instance, and these can be summed to yield the surface tension. It is possible to take these components which have been generated by the empirical expressions and draw (2D) maps of wetting.
The experimental programme required to produce the necessary information is relatively simple and follows the rationale described in Section 2. The contact angles for a solution on two standard substrates, for instance glass and poly (vinyl chloride) (PVC), are determined. One of the surfaces is polar and the other is non-polar. Following this the contact angles of two standard liquids on the substrates are determined (iodomethane and water, for instance). The contact angle on the substrate of the liquid of particular interest is subsequently determined. From this information the polar and dispersive components are derived by using the Owens.
Wendt equation. For the unknown sample these components are plotted against each other. An example plot is shown in Figure 1.22
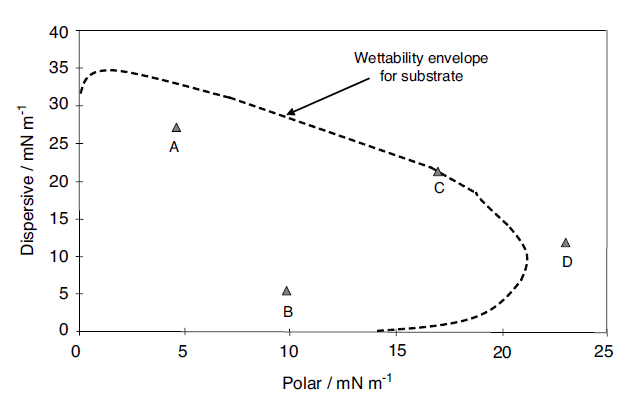
Fig. 1.22 Wettability envelopes for a substrate with a series of liquids
The dispersive component is plotted along the y-axis against the polar component along the x-axis. Four points labeled A, B, C and D are shown on the plot. An envelope, the ‘wettability envelope’, is also plotted. The envelope is created when the Owens–Wendt model is solved for the case of a contact angle of 90°; So the area bounded by the axes and the curve is less than 90° and that outside this boundary is greater than 90°. For each of the four liquids it can be seen that A and B will wet the substrate. From this it is clear that the two materials A and B, which have different overall surface tensions, can be plotted on a map, and both can be seen to be wetting. The values of polar and dispersive contributions have been calculated previously. This starts to give an understanding of wettability. It is also clear that D is de-wetted, since it sits outside that envelope. In the case of liquid C it has a contact angle of 90° and so is on the border of wetting and de-wetting. It is possible to make a comparison here between this type of approach and the calculation of solubility parameters. The Hildebrandt solubility parameter [103] gives a single value of solubility, whereas it is also possible to break the solubility parameter into components, as is done in the Hansen solubility parameters [103,104], or partial solubility parameters. In the latter a three-component coordinate set of parameters can be identified, which map out the solubility in a more detailed manner and give a greater insight into the solubility of materials, polymers for instance, in different solvents. Thus the solubility of a material is put onto a 3D map which has axes of polar, dispersive and hydrogen bonding. The same principle is adopted here, but using surface tensions, to see how wettability is influenced by the components of surface tension. Other models such as Wu1, and Wu2, can also be used to draw these envelopes. This gives another view and method of predicting the wetting behavior of substrates with liquids.
4.2 Intrinsic equilibrium contact angle (IECA)
In addition to experimental procedures to determine the thermodynamic equilibrium contact angle, it can also be evaluated from the measured advancing and receding contact angles as derived by Radmor [105, 106] by the relation of the as-placed contact angle to drop size.
The combination of the Young equation and the Wenzel equation gives the relation between the surface tensions and the global energy minimum equilibrium contact angle θ0 for the liquid drop:
![]() (1.78)
(1.78)
where ![]() are the interfacial tensions (or interfacial energies [107–109]) between phases i and j , and the indexes S, L and V stand for solid, liquid and vapor, respectively (though vapor may sometimes refer to another liquid medium surrounding the drop). The reason a drop can have a contact angle that is different from θ0 is related to the pinning of the three phase contact line to its position which induces a force resisting drop motion. One can describe the force per length associated with this pinning, k/r, by Eq. (1.79) (see [110-115]) (where r is the radius of the circle the drop makes with the surface). In this description k has opposite values, kA and kR corresponding to advancing and receding contact angles:
are the interfacial tensions (or interfacial energies [107–109]) between phases i and j , and the indexes S, L and V stand for solid, liquid and vapor, respectively (though vapor may sometimes refer to another liquid medium surrounding the drop). The reason a drop can have a contact angle that is different from θ0 is related to the pinning of the three phase contact line to its position which induces a force resisting drop motion. One can describe the force per length associated with this pinning, k/r, by Eq. (1.79) (see [110-115]) (where r is the radius of the circle the drop makes with the surface). In this description k has opposite values, kA and kR corresponding to advancing and receding contact angles:
![]() (1.79a)
(1.79a)
![]() (1.79b)
(1.79b)
where rA and rR are drop radii that correspond to the advancing and receding curvatures and γ ≡ γLV.
From this, the relation between the θA, θR and θ0 is given by [111]
![]() (1.80)
(1.80)
where
![]() and
and ![]()
Equation 1.69 has been derived from a combination of Young and Wenzel equations and recognizing that the equilibrium contact angle results from the global energy minimum in the system [105,106]. The advancing and receding contact angles result from pinning of the three-phase contact line, resisting motion of the drop. He assumed that the resistance to the motion out for advancing drop was just equal to the resistance to the motion in of the receding drop. This is because both of these resistance are due to the three-phase contact line pinning to the similar protrusions.[105] in other words, the irregularities on the surface are isotropic with respect to their nature and distribution [105,106]. However, this is rather a weak assumption in the derivations.
Hot keywords of USA KINO:contact angle, contact angle measurement, contact angle meter, contact angle goniometer, surface tensiometer, interfacial tensiometer, surface tension measurement, surface tension, surface tensiometry, contact angle measurement equipment and device, calculating surfac free energy, Determining Critical Micelle Concentration (CMC) of surfactant, made in China Method for choosing surface tensiometer NEW Method for choosing contact angle meter (goniometer) NEW Method for choosing interfacial tension meter NEW

Manage technical support: www.chem17.com GoogleSitemap
MainPro : contact angle,contact angle meter,contact angle goniometer,surface tension,surface tensiometer