1, Background
Surface tension or interfacial tension is the macroscopic manifestation of a host of molecular phenomena at the interface between liquid-fluid (or liquid-gas) system. Surfactants (or surface active agents) may change a liquid's wetting characteristics, and alter surface tension and mass transfer at liquid interfaces. The usual interpretation of surface tension as the force per unit length exerted across any line lying in the plane of the liquid surface has led to the development of a variety of force-balance surface or interfacial tensiometers. The distinction between surface tension and surface free-energy per unit area (Ip and Toguri 1994) is unessential here. These devices typically rely on placing a solid object into the liquid of interest, determining the length of the macroscopic solid-liquid contact line (hereafter referred to as the wetted perimeter), and measuring the added force on the object resulting from its contact with the liquid. The interfacial surface tension is then recovered by dividing the measured force by the wetted perimeter. Implicit in these techniques are the assumptions that: i) surface tension does not depend on liquid-surface curvature, ii) the liquid does not apply any force to the submerged portion of the solid beyond hydrostatic pressure, and iii) the angle that the interface makes with the vertical at the contact line is known (usually assumed to be zero for the receding contact angle in the experimental determination of surface tension).
Surface tensiometer is frequently associated with extraordinary experimental hygiene. Yet the surface tension of ordinary tap-water/air interfaces subject to air-borne particulate contamination is still of interest in many hydrodynamic studies involving large wave tanks or towing basins where high-purity water cannot be used and even daily water changes are not practical. Here, vertical-pull film balances are superior to horizontal or Langmuir film balances (Harkins and Anderson 1937) and surface properties must be monitored in situ because any type of sampling will disturb any intentional or unintentional surfactants. Unlike some surface or interfacial tensiometer (tensiometry) methods, the technique described here is robust in ordinary laboratory environments and yields consistent results across a variety of wetted-object geometries even when high-purity liquids and clean-room conditions are unavailable.
Accurate surface tension measurements with force balances have proved difficult because the results depend on the contact condition between the object ( such as plate or ring, rod) and the liquid interface, the shape of the meniscus (contact angle? And it is actually differ from that of sessile drop method. Visit www.uskino.com and find surface tensiometer model 80 series for more information about contact angle correction method.), the object's buoyancy (refer surface tension meter model A80 series), and other possible molecular attraction or repulsion forces between the object and the liquid. These problems have been ignored through simplifying assumptions, treated by ad hoc corrections or special ways, mitigated by constraining the measurement technique, or partially corrected by additional measurements. These remedial actions typically prevent in situ measurements or complicate the overall technique reducing its utility and flexibility. More elaborate surface tension measurement techniques have been pursued, but these are application specific and require more resources and process time than is typically available for basic surface tensiometer.
There are two main techniques for force-balance surface / interfacial tensiometry ( tension meter): the Wilhelmy plate, and DuNouy ring methods (Adamson 1990; Gaines 1966; Davies and Rideal 1963). These are discussed in the next two subsections. The final subsection covers other force-balance techniques. Additional information is available in Rusanov and Prokhorov (1996).
2, Wilhelmy plate method
There are several variations of the Wilhelmy plate methods. All are based on balancing the static forces of surface tension, gravity, and buoyancy acting on a thin plate (usually made of glass or platinum) suspended vertically in the air-liquid interface. Figure 1 shows a cross sectional free body diagram of the active part of the balance while for a known wetted plate perimeter, the experimentalist measures the pull on the balance, and, in some cases, the vertical position of the bottom plate edge relative to the undisturbed free surface. The surface tension σ is then determined from (Allan 1958; Jordan and Lane 1964)
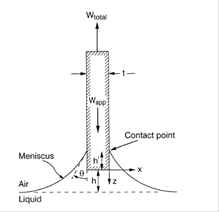
Fig. 1. Free body diagram of the Wilhelmy plate balance. The total pull on the plate of thickness t and length L (into the page) is balanced by its own weight, the force from surface tension at the contact line, and the negative buoyancy resulting from raising the plate above the mean free surface a distance h. The angle from the vertical h of the meniscus in contact with the plate is a true contact angle when capillary rise up the plate occurs (h’≠0). For the case of no capillary rise, h’ is zero
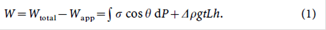
Here, Wtotal is the weight registered by a hook balance, Wapp is the dry weight of the apparatus (plate and the harness), P is the wetted perimeter of the plate, σ is surface tension, h is the angle the liquid meniscus makes with the vertical at its point of contact with the plate, Do is the density difference between the liquid and the air, g is the gravitational acceleration, t and L are the plate thickness and length (for a rectangular plate P=2(L + t) ), and h is the height of the bottom of the plate above the undisturbed mean surface. The angle with the vertical θ is a generalization of the macroscopic or apparent contact angle that remains well-defined at a solid surface discontinuity. The contact angle is the angle defined by Young's equation (Adamson 1990). When a meniscus contacts an object at a corner and no capillary rise up the vertical sides of the object occurs (h’= 0), h is well defined but the contact angle is not. For the frequently encountered case where some capillary rise occurs (h≠’0), h is both the contact angle and the angle with the vertical. All the parameters in (1), exceptσ, θ, and h, are easy to determine accurately. The final term in (1) is called the buoyancy correction. While not large, typically 1 to 10% of Wtotal , the buoyancy correction is typically not negligible (Gaonkar and Neuman 1984). Note that surface curvature effects indirectly enter (1) through the contact angle θ.
Four variations of the Wilhelmy plate measurement are commonly used: the zero-buoyancy method, the detachment method, the immersion method (Gaines 1966), and the maximum-pull method (La Mer and Robbins 1958; Loglio et al. 1976; Gaonkar and Neuman 1984). In principle, the four variations are similar except for procedural adjustments that simplify the final two terms in (1) so only the first two are considered here. The immersion method gave inconsistent results and the maximum-pull method failed since the meniscus always ruptured before the pull reached a maximum for the thin plates we considered.
2.1 The zero-buoyancy method for measurement of surface tension or interfacial tension
In this method, the plate is quasi-statically lowered while keeping the lower plate edge parallel to the plane of the undisturbed liquid surface until the slide first contacts the liquid surface (Padday 1957; Zotova and Trapeznikov 1960; Padday and Russell 1960; Slowinski and Masterton 1961; Pallas and Pethica 1983; Gaonkar and Neuman 1987). The surface tension induced force is then measured under the assumption that h is zero. However, the advancing contact line leads to variability in the contact angle θ. This method is susceptible to significant error if the measured pull at first contact is used. Instead, the plate should be further lowered into the fluid and then withdrawn to the first-touch height to promote better plate wetting (Kawanishi et al. 1970; Lane and Jordan 1970).
2.2 The detachment method (Furlong and Hartland 1979) for measurement of surface tension or interfacial tension
In this method, the plate is quasi-statically pulled from the liquid until the meniscus ruptures. Withdrawal of the plate ensures wetting through a receding contact line that drives h toward zero. The hope is that θ approaches zero on the entire plate perimeter as the contact line comes toward the corner near rupture. A thin plate ensures that the buoyancy term is small and that there cannot be much under-cutting of the meniscus before rupture occurs. The detachment method is subject to uncertainty arising from non-repeatability of dynamic meniscus rupture (Padday and Russell 1960; Padday 1969, Loglio et al. 1976).
The most common implementation of either Wilhelmy plate method assumes that the free surface is vertical at the point of attachment (or close enough to justify cos θ=1) and that the buoyancy term can be neglected for a sufficiently thin plate. Hence, Eq. (1) reduces to

The two neglected effects leading to Eq. (2) partially cancel, and this has led to a lack of consistency between sources about the terms in Eq. (1) that are prudently modified or neglected.
The use of smooth or roughened plates to enhance plate wetting is controversial (Kawanishi et al. 1969). Some investigations generally support roughening plates (Princen 1970; Furlong and Hartland 1979; Gaonkar and Neuman 1987), while others generally oppose it (Jordan and Lane 1964; Lane and Jordan 1970, 1971; Pallas and Pethica 1983). Some investigators motivated by practicality (Pike and Bonnet 1970), like ourselves, merely use the finish obtained on commercially available glassware.
Additional controversy surrounds the necessity of an empirical correction. In some studies (Jordan and Lane 1964; Pike and Bonnet 1970; Lane and Jordan 1971; Furlong and Hartland 1979), as well as the present, a “film deficit” is observed near the plate ends. The consequence of this variation in meniscus shape is a perimeter-location dependent value of θ which causes measured surface tension values to have an unexpected dependence on plate thickness. This θ variation is commonly ignored or dismissed (Taylor and Mingins 1975; Orr et al. 1977; Furlong and Hartland 1979; Pallas and Pethica 1983; Sauer and Carney 1990; Palas and Harrison 1990; Mennella and Morrow 1995), or treated with
an empirical end or peripheral correction (Padday 1957, 1969; Padday and Russell 1960; Kawanishi et al. 1970; Pike and Bonnet 1970; Gaonkar and Neuman 1984, 1987). Apparently, this end-correction controversy will not soon be settled either by experiments (Pallas and Pethica 1989, 1991; Gaonkar and Neuman 1991; Pallas and Pethica 1991) or three-dimensional theory (Orr et al. 1975, Orr et al. 1977).
3, surface tensiometer base on Du Nouy ring method for measurement of surface tension or interfacial tension
The Du Nouy ring method may be the most common force balance method. Here, a platinum, wire ring lying in a plane parallel to the liquid surface is submerged in the liquid and then slowly withdrawn while the net fluid force on the ring is measured. In general, the ring with attached liquid meniscus is raised above the mean undisturbed surface until the pull on the ring reaches a maximum. Further raising of the ring causes a reduction of pull. The maximum force, Wmax obtained during ring withdrawal can be directly related to the surface tension if the ring is perfectly wetted by the fluid (Harkins and Jordan 1930; Freud and Freud 1930; Cini et al. 1972; Huh and Mason 1975). However, a non-zero contact angle has been found to be important for ring surface tensiometer ( or tensiometry ) (Princen and Mason 1965; Cram and Haynes 1971; Gifford 1978). Hence, one needs a priori knowledge of the contact angle to properly implement the Du Nouy ring method, so the Wilhelmy plate method is often recommend for work where liquid wetting characteristics are not known (Padday and Russell 1960; Gaines 1966; Gaonkar and Neuman 1984; Adamson 1990).
Flaming the du NouK y ring (or platinum Wilhelmy plates) is a controversial cleaning procedure. Many investigations support flaming (La Mer and Robbins 1958; Lane and Jordan 1970; Cini et al. 1972; Huh and Mason 1977; Furlong et al. 1983), while others (Gaines 1960; Kawanishi et al. 1970; Gaonkar and Neuman 1984) claim that the procedure affects the wetting and thereby affects the surface tension measurement.
Another problem common to the ring (and the plate) is the interpretation of the actual force measurement. Equating the force on a Du Nouy ring just before meniscus rupture to any of the points on the force versus height curve produced from theory to determine the surface tension is not recommended (Padday and Russell 1960; Padday 1969; Huh and Mason 1975). Perhaps the largest single source of misunderstanding in surface tensiometer (tensiometry) is confusing Wmax with the experimentally determined point of meniscus detachment. The experimental point of meniscus detachment may occur anywhere along the force versus height curve as determined by ®lm stability and the detailed procedures of the particular force balance method. A typical torsion balance either controls h or W, or both, and usually uses the force immediately prior to detachment in the measurement. Some methods are designed to cause meniscus detachment as close as possible to Wmax, however, the actual proximity is always in doubt once rupture occurs. Certain geometries, like
the thin Wilhelmy plates used in this study, cause meniscus rupture before Wmax is reached.
4, Diagram of different measuring methods of surface tensiometer
4.1 Modified Wilhelmy plate method
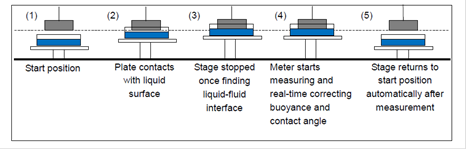
4.2 Classical Wilhelmy plate method (Max pull)
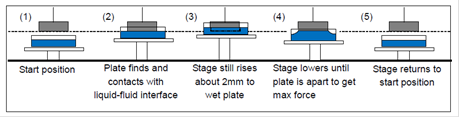
4.3 Classical Wilhelmy plate method (Zero buoyance method)
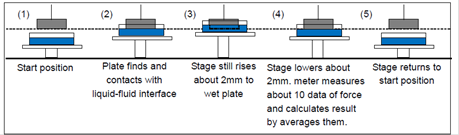
Note:This method is used in surface tensiometer made by Kruss, KSV, KYOWA. And it cannot used to measure surface tension of cationic surface active agent and sample with viscosity due to its immersing and drawing out process.
4.4 DuNouy ring method
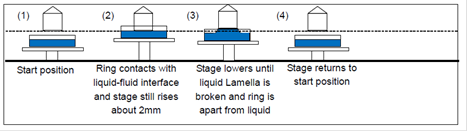
Note: Sometimes, we will repeat process 2, 3 after process 3 by rising stage and lowering stage several times, and calculate surface tension by average measured data.
Hot keywords of USA KINO:contact angle, contact angle measurement, contact angle meter, contact angle goniometer, surface tensiometer, interfacial tensiometer, surface tension measurement, surface tension, surface tensiometry, contact angle measurement equipment and device, calculating surfac free energy, Determining Critical Micelle Concentration (CMC) of surfactant, made in China Method for choosing surface tensiometer NEW Method for choosing contact angle meter (goniometer) NEW Method for choosing interfacial tension meter NEW

Manage technical support: www.chem17.com GoogleSitemap
MainPro : contact angle,contact angle meter,contact angle goniometer,surface tension,surface tensiometer