Measurement of contact angle and interface tension--method and ways

 Numerous methodologies have been developed for the measurement of interfacial properties including contact angles and surface tensions. Contact angles are most commonly measured by aligning a tangent with the profile of a sessile drop at the point of contact with the solid surface. Liquid surface tension measurements commonly involve the determination of the height of a meniscus in a capillary or on a fiber or a plate. There are some of the major methods including the Wilhelmy plate technique and Du Noüy ring method, the drop weight method, the oscillating jet method, the max bubble pressure method, and the spinning drop method. Further consideration of this topic is outside the scope of this manual. More information can be obtained from Lyklema (2000) and Adamson and Gast (1997). Alternative approaches to obtain the interfacial properties are drop shape methods developed to determine the liquid–vapor or liquid–liquid interfacial tensions and the contact angle from the shape of a sessile drop, pendant drop, or captive bubble. These methods are widely used due to their simplicity and accuracy. In this section, the drop shape methods are described in detail.

2.1 Measuring the contact angle

Measurement of contact angles appears to be quite easy when first encountered, but this can be misleading and the accurate measurement of thermodynamically significant contact angles requires painstaking effort. If the substrate is not prepared properly, if very pure liquids are not used while forming drops and if some important practical issues during measurement, such as drop evaporation, the location of the needle in the drop, and maintaining a sharp image, are not considered, then incorrect and generally useless contact angle results can be obtained, which may be used as “evidence” for false thermodynamical conclusions. Many different methods have been developed for the measurement of contact angles, but only a few are popular today. Two preferred approaches are: the measurement of the static or dynamic contact angle of a sessile drop (captive drop) on solid surface using a video camera or goniometer; and the dynamic contact angle measurement method using tensiometry, which involves measuring the forces of interaction, while a dynamic (moving) flat solid plate is immersed into or withdrawn from a test liquid.

2.1.1 The contact angle lexicon

The general, operational definition of the CA was given in the introduction. However, there are sub-definitions of CAs that need to be used under various circumstances. This section describes them in a concise form, in order to serve as a quick reference and enable easy comparison.

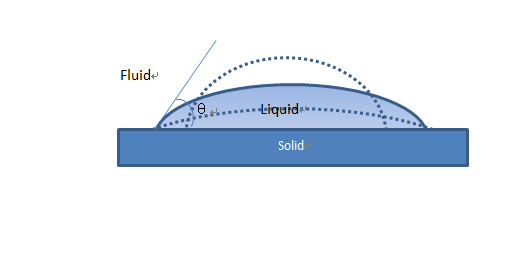
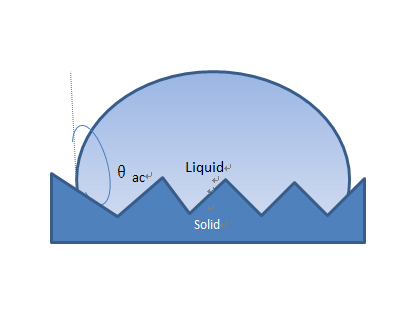
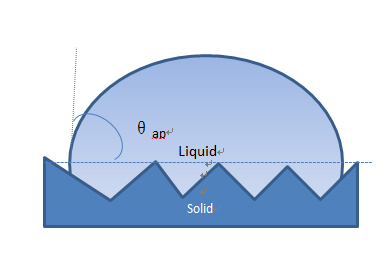
Fig. 1.10 Contact angles: (a) Various geometric contact angles for same volume of drop;(b) the actual contact angle (intrinsic contact angle); (c) the apparent contact angle.

• Geometric Contact angle, θ, (fig 1.10 a) is the one calculated using geometric considerations only, regardless of whether the system is at equilibrium. It serves as an independent variable for calculating all possible Gibbs energy states of the system.
• Ideal contact angle, θ_i, is the equilibrium contact angle that a liquid makes with an ideal solid surface. The latter is defined as smooth, rigid, chemically homogeneous, insoluble, and non-reactive surface. The ideal CA is also sometimes referred to as the intrinsic or inherent contact angle.
• Young contact angle, θ_Y, is defined by the equation conceived by Young (Eq. 1.2). For most macroscopic systems, the Young CA represents the ideal CA; however, as argued, for systems of surfaces with very small radii of curvature, they may be different due to line tension. The Young CA depends only on the physico-chemical nature of the three phases, and is independent of both the system geometric shape and gravity. The latter may affect the shape of the liquid-fluid interface, but not θ_Y.
• Actual contact angle, θ_ac, is the local equilibrium CA at a point on a solid surface that may be rough or chemically heterogeneous (Fig 1.10 b) . For most macroscopic system, the actual CA is equal to the Young CA; however, when line tension is meaningful, they may be different.
• Apparent contact angle, θ_ap, is an equilibrium CA measured macroscopically on a solid surface that may be rough or chemically heterogeneous. The detail topography of rough solid surface cannot be viewed with regular optical means; therefore, this CA is defined as the angle between the tangent to the liquid-fluid interface and the apparent solid surface, as macroscopically observed (Fig 1.10 c). θ_ap is actually an equilibrium value of geometric CA, θ. It is important to note that, as shown schematically in Fig 1.10 c, the apparent and actual CAs may be very different. There exists a range of discrete apparent CAs for any non-ideal solid surface.
• Advancing contact angle, θ_a, is the highest possible apparent CA that can be achieved for a given wetting system (usually it is realized by increasing the volume of drop (refer Neumann approach)). The advancing CA is an equilibrium (though metastable) CA, since θ_ap is, by definition, an equilibrium CA.
• Receding contact angle, θ_r, is lowest possible apparent CA that can be achieved for a given wetting system (usually it is realized by decreasing the volume of the drop). Similarly to the advancing CA, the receding CA is an equilibrium (though metastable) CA.
• Most stable contact angle, θ_ms, is the apparent CA that is associated with the lowest possible Gibbs energy of the wetting system. The value of this CA is expressed, under appropriate conditions by Wenzel, Cassie, or Cassie-Baxter equations.
• Static contact angle: We can also call it as geometric CA or apparent contact angle, θ_ap. The measuring condition (such as volume, boundary surface or solid surface) will not be changed anthropogenic when the drop (or bubble for captive bubble method) is placed on solid surface.
• Dynamic contact angle: It is the one measured when there is relative motion between the liquid and the solid at appreciable velocities. Usually measurement of dynamic contact angle includes advancing contact angle, receding contact angle and rolling off contact angle. Its value depends on the contact line velocity. In order to avoid ambiguity, this term should not be used for CAs measured by pushing the liquid very slowly in order to obtain advancing or receding values. For such measurements, the term quasi-static seems to be the most appropriate.

2.1.2 Measuring static contact angle

The most widely used method is to measure the angle of a sessile drop resting on a flat solid surface using a goniometer–microscope equipped with an angle-measuring eyepiece or, more recently, a video camera equipped with a suitable magnifying lens, interfaced to a computer with image-analysis software to determine the tangent value precisely on the captured image. A suitable cold light source and a sample stage whose elevation can be controlled to high precision are also required for the application of this technique. Formerly, the drop profile was photographed and the tangent of the sessile drop profile at the three-phase contact point drawn onto the photo-print to determine the value of the contact angle. At present, commercial instrument adopt image recognition and curve fitting technology and it can greatly enhance the precise of measurement of static contact angle. So, newer instrument with these technologies may be named as drop shape analysis system. 

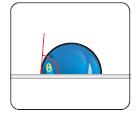
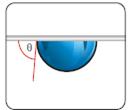
Fig. 1.11 sessile drop (left picture) and captive bubble drop (right picture)

Generally, there is three generation of measuring method for static contact angle.

- First generation is used microscope with angle indexes to measure the contact angle manually just by putting the tangent along the drop shape;

- The second generation is used capturing system to take photograph and calculating by putting key point of θ/2 (W/H) method or  circle fitting method. These two generations are usually named as goniometer;

- The third generation is named as drop shape analytical system as described above and it is more reliable and precise.

In static θ measurement, the results are somewhat dependent on the experience of the operator and interactions at surface boundary, such as evaporation of liquid drop, migration of surfactants, absorbing of liquid and chemical reactions, etc.. So the static contact angle or equilibrium contact angle of this state is relative and contact angle depended on times is recommendation for carrying out.

General procedure of measuring static contact angle includes dosing and transferring drop to surface of solid, capturing the drop image of continuous capturing the images depended on times, recognizing the drop image such as detecting the drop profile and drop edge, fitting the drop profile by selecting curve equation such as circle, Young-Laplace equation, etc..

2.1.3 Measuring dynamic contact angle

The measurement of a single static contact angle to characterize the solid–liquid interaction is not adequate because, in practice, there is no single equilibrium contact angle, θe, on a solid surface. While deriving Young’s equation, we assumed an ideal solid that is chemically homogeneous, smooth, rigid, and flat to an atomic scale. It should also be chemically and physically inert with respect to the liquids to be employed. Ideally, according to Young’s equation, a unique contact angle is expected for a given system (e.g. a liquid drop on a solid surface). In a real system, however, a range of contact angles is usually obtained instead. The upper limit of the range is the advancing contact angle, θa, which is the contact angle found at the advancing edge of a liquid drop. The lower limit is the receding contact angle, θr , which is the contact angle found at the receding edge. The difference between the advancing and receding contact angles is known as the contact angle hysteresis, θ_hyst

θ_hyst ＝θa－θr                                                                (1.21)

Practically, all solid surfaces exhibit contact angle hysteresis and because of this hysteresis, the contact angle interpretation in terms of Young’s Eq. (1.2) is contentious. Not all the experimentally measured or observed contact angles are reliable and appropriate. Although contact angle hysteresis has been studied extensively in the past several decades, the underlying causes and its origins are not completely understood. Studies have attributed contact angle hysteresis to surface roughness and heterogeneity, as well as metastable surface energetic states. Some found that the hysteresis decreases with increasing molecular volume of the liquid on monolayers. In more recent studies, contact angle hysteresis was found to be related to molecular mobility and packing of the surface, liquid penetration and surface swelling.

There are three common ways for measuring dynamic contact angle

(1) increase and decrease volume of liquid and with needle inside the drop:

-   When a liquid drop is formed by injecting the liquid from a needle connected to a syringe onto a substrate surface, it is allowed to advance on the fresh solid surface and the measured angle is said to represent the advancing contact angle, θa. For each drop–solid system there is a maximum value of θa before the  three-phase line is broken (it should be noted that the stainless steel needle must be kept in the middle of the drop during measurement of θa, on the metal needle surface; alternatively, plastic needles such as Teflon and polypropylene may be used with water). Sometimes, we use increasing of length of contact line to estimate forming of advancing contact angle.

- The receding contact angle, θr, can be measured when a previously formed sessile drop on the substrate  surface is contracted by applying a suction of the drop liquid through the needle. Precise measurement of θr is very difficult.

These contact angles fall within a range where the advancing contact angles approach a maximum value and receding angles approach a minimum value (θa>θr). Alternately, both advanced and receded angles are measured when the stage on which the solid is held is tilted to the point of incipient motion of the drop.

Both θa and θr depend on the surface roughness (detailed shapes and configurations of the patches or strips) and also on the surface chemical heterogeneity. The direct determination of θa within ±2° is easy, but it is difficult to reduce the relative error to ±0.5°. This is because the direction of a liquid profile rapidly changes with the distance from the three phase contact point. The difference between θa and θr gives the contact angle hysteresis, H, (H ≡θa −θr), which can be quite large, around 5–20° in conventional measurements (or 20–50° in some exceptional cases).

The problem of this approach is distortion of the drop surface caused by the needle. If the needle enters the drop at a point very close to the solid, it may obscure the drop profile. It is best to keep the needle at the middle of the drop. If the needle passes through the upper surface of the drop, there will be some capillary rise of the liquid up the needle and distortion of the surface. (However, it has been claimed by some authors that this capillary rise does not perturb the liquid in the region of the contact line with the solid.) Removing the needle from the drop does not help, because that makes it impossible to study hysteresis. Another problem is the fitting method for this situation is usually used tangent method (such as straight line or similarly polynomial equation such as y=a+bx+cx^0.5+d/lnx+e/x²) and it may lead to high data error, small reliability due to its simplified fitting method. Spline fitting method and Realdrop^TM method adopted in CAST®3.0 may enhance the precision but this (enhance-effect) is not very significant. The third problem is the variable rate of introducing the drop liquid through the needle during determination of θa and the variable rate of withdrawal of the liquid during determination of θr. The sessile drop method is not particularly well adapted to quantitative measurement of the dependence of contact angle on the rate of advance or retreat, because a linear rate of change in drop volume does not correspond to a linear rate of motion of the drop front. An appropriate rate is of the order of 0.01–0.10mmmin−1 linear advance or retreat by using a motor-driven syringe. Also, it is best to specify a constant time allowed before measuring the contact angle after the motion stops, e.g. 1–10 sec, to damp the drop oscillations formed in order to obtain more precise data.

(2) Rotating sample stage:

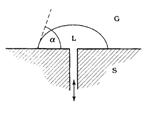
A sessile drop is formed on a plate of solid substrate gripped at one end onto a motorized or manual rotation stage, which can be rotated to the point of incipient motion of the drop. When the plane of the solid surface reaches a critical slope, the drop starts to roll off. The measured angle at the downhill edge of the drop approaches θa, and the angle at the uphill edge approach θr, as shown right. The angles should be measured immediately prior to the drop starting to slide. The roll-off angle, θroll-off, can also be used to derive thermodynamic conclusions; however, this method is not very reliable, because the determination of a clear and sharp drop image at the instance of sliding is difficult, and also it gives inconsistent results with rough substrates which show a strong pinning behavior with the liquid drop, so that no drop sliding occurs even at a tilt angle of θt = 90°. In addition, some researchers cautioned against this method because it yields values of θa and θr that are strongly dependent on the drop size.

(3) increase and decrease volume of liquid and with sample made a hole for dosing or sucking liquid:

This approach is preferred for you due to its reliable and precise and algorithm that CAST®3.0 adopts is ADSA^TM exactly. It is first promoted by Neumann and co-workers. They made a small hole in the flat substrate sample and first deposited a small drop on the substrate through a needle connected to this hole beneath the substrate. The size of the drop is then increased by feeding more liquid to the drop by means of this needle connected to a motorized syringe. This procedure prevents the drop oscillating and also destruction of the axisymmetric. By this means, they controlled the rate of advance or retreat of the symmetrical sessile drop on the substrate, to measure θa and θr precisely. They also developed a method to determine both the contact angle and surface tension of the liquid by applying a digital image analysis to drop profiles and a computation method named axisymmetric drop shape analysis, ADSA. In this method, an objective function is constructed which expresses the error between the physically observed profile and the theoretical Young-Laplace equation curve; the function is then minimized using an iterative procedure.

The limitation of this method is some solid sample such as glass cannot make a hole easily.

2.1.4 Captive bubble method

A captive air (or other gas) bubble is formed in the liquid contacting with the solid by means of an inverted micrometer syringe beneath the substrate which is kept in the test liquid. The contact angle is measured by means of a goniometer microscope or video camera. In this method, the solid–vapor interface is in equilibrium with the saturated vapor pressure of the liquid, which is present in the bubble. When more air is added to the bubble through the needle, the surrounding liquid front retreats and gives an angle which is equivalent to θr in the conventional sessile drop method in air. Withdrawing the air from the bubble causes the liquid front to advance, which is equivalent to θa. It is interesting to note that the θe measured in the captive bubble method is nearer to θr than to θa. And this method is usually used to measure the surface of super-hydrophobic (＞170° )  or super-hydrophilic (＜3° ), as well as measurement of low interface tension of liquid-fluid system.

2.2 Method for evaluating the drop shape and calculating contact angle

Calculating contact angle based on drop shape method usually includes 4 steps: (1) capture the drop image and saving it into disk or memory; (2) detecting drop shape profile using edge detection and image segmentation method, then, drawing the drop profile; (3) fitting a mathematical model for the detected drop profile;(4) calculating the contact angle based on the fitted mathematical equation and detected base line. The various method of calculating the contact angle therefore differs in the mathematical model used for fitting the drop shape. The scope of application of various methods is different due to its own strengths and weaknesses. So, you should choose appropriate method according to the real test requirements. All methods calculate contact angle as tanθ at the intersection of fitted drop profile and the solid base line.

2.2.1 θ/2 method (W/H method): Using complete drop shape

Dosing and transferring a drop with volume of 1-5uL to form a drop on the solid surface, liquid drop will become round by its own surface tension and eventually shapes into part of a sphere. The shape of drop with large volume cannot form a sphere due to the effect of gravity. So, the best volume of this method is about 1-5uL and effect of gravity will be ignored. When volume more than 10uL，θ/2 is always useless and may lead to a misunderstanding. The smaller drop volume, the more accurate the approximation for smaller drops.

In calculating process, software finds three key points such as left end point, right end point and apex of drop using image recognition technology based on captured image. The diameter (2r) (width of drop) and height (h) of this drop are obtained by finding the defined coordinates of these points, and contact angle θ is calculated with equation given below.

If droplet forms part of a sphere (in 3D), and profile of drop in 2D is circle, and the following can be proven by the theorem of geometry 

(1) If segments, points and angles are as shown while drop forms part of an arc, the following definitions can be formulated: 

, , ,

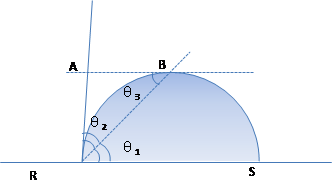
(2)Then:θ1 × 2 = θ

(3) tanθ₁=h／r  → θ = 2*atan (h／r)                                                 (1.22)

The advantage of θ/2 method is simply to adopt and faster calculating speed. But, θ/2 method is not suitable for measurement of dynamic contact angle due to the drop height cannot be determined accurately when the needle is still in the drop or drop shape is not as circle when drop is tilted. This method also has the disadvantage that the drop with small volume is necessary, but drop volume less than 5uL cannot be transferred to solid surface with super-hydrophobic.

2.2.2 Circle fitting method: Using complete drop shape

As described in the θ/2 method, circle fitting method assumes the shape of formed drop on solid surface is a part of a sphere (in 3D) ( profile of drop in 2D is circle). Action of forces such as gravity may often be neglected in comparison to surface tension effects. So, dosing and transferring a drop with volume of 1-5uL is also required. Differing from θ/2 method, circle fitting method calculates the contact angle as procedure described below:

- Capture the drop image and saving it into disk or memory;

- Detecting drop shape profile using edge detection and image segmentation method, then, drawing the drop profile;

- Detecting the base line using corresponding algorithm;

- Fitting circle curve for the detected drop profile and finding the equation of circle;

- Calculating the contact angle based on the fitted circle equation and detected base line.

Circle fitting method is the most widely used method for calculating the contact angle due to its high accuracy. It is especially applicable for calculation of contact angle with value under 30°. Its disadvantage is same as θ/2 method that described upper.

2.2.3 Ellipse fitting method: Using complete drop shape

Ellipse fitting method does not need to assume of circular-like profile of drop shape. It is used ellipse curve for fitting of the drop profile instead of circle curve that described upper and calculating process is similar to latter. The difference is that the algorithm of ellipse fitting is very complicated. It can be used to calculate contact angle based on sessile drop with very wide range value (0-130°).

Its disadvantage is this method calculates contact angle just using mathematic algorithm, no more theoretical derivation. This may lead the deviation between test Value and actual value. Another disadvantage is this method is not suitable for measurement of dynamic contact angle due to the drop height cannot be determined accurately when the needle is still in the drop or drop shape is not as circle when drop is tilted.

2.2.4 Young-Laplace equation fitting method (ADSA-P^TM): Using complete drop shape

Young-Laplace equation fitting method (ADSA-P) is a most complicated technique to determine liquid-fluid interfacial tensions and contact angles nom the shape of axisymmetric menisci, i.e., from sessile as well as pendant drops. Assuming that the experimental drop is Young-Laplace and axisymmetric, ADSA-P find the theoretical profile that best matches the drop profile exacted from the image of a real drop, from which the surface tension, contact angle, drop volume and surface area can be computed. The strategy employed is to fit the shape of an experimental drop to a theoretical drop profile according to the Young-Laplace equation of capillarity, using surface / interfacial tension as an adjustable parameter. The best fit identifies the correct surface / interfacial tension from which the contact angle can be determined by a numerical integration of the Young-Laplace equation (1.20). Details of the methodology will be discussed next. ADSA-P has been used to perform accurate measurements of the surface tensions and contact angles in a variety of situations. It can be used for both air-Liquid and liquid-Liquid systems; it is particularly suited for the study of time-, temperature- and pressure-dependence of interfacial tensions and contact angles.The disadvantage of this method is it assumes a symmetric drop shape; therefore it cannot be used for dynamic contact angles where the needle remains in the drop, especially for receding contact angle. But you can select the approach that made a hole in solid surface to measure the dynamic contact angle. This method is especially suitable for measuring contact angle of super-hydrophobic surface due to its taking gravity during calculating process.

2.2.5 Quadratic polynomial fitting method: Using part of drop shape

This method only cares about part of drop shape nearby the contact point. Calculating process is also similar to circle fitting or ellipse fitting method, and the difference is, in this method, a quadratic polynomial function is fitted to a section of the profile in the region of the baseline of drop.

In quadratic polynomial equation fitting method, a number of points from the contour of a drop near to the contact points are extracted and fitted by a polynomial using least square method, and then we can solve the equation. From the slope of the quadratic polynomial equation at the contact point of 3-phase, contact angle can be calculated from included angle between the tangent and the baseline.

The disadvantage of this method is this function is just the result of numerous theoretical simulations; it is sensitive to disturbing in the contact section of drop profile that caused by contaminants or surface irregularities at the contact section. As only part of drop profile is evaluated, this method is very suitable for dynamic contact angles. Nevertheless, this method requires an excellent image quality, especially in the region of contact section.

2.2.6 Spline curve fitting method: Using complete or part of drop shape

This method is most useful as it is resilient. A spline curve is used to fit complete or part of drop shape, and contact angle can be calculated via the fitting method described in Quadratic polynomial fitting method.

It can be used to calculate all kinds of angle such as irregular contact angle of adhesive drop, dynamic contact angle, etc.

2.2.7 Curve ruler method: Using part of drop shape

There are about 17 kinds of curve fitting method in cure ruler method. Contact angle can be calculated via the fitting method described in Quadratic polynomial fitting method. Among them, double circle ruler is especially suitable for the measurement of dynamic contact angle due to it perfect fitting ability.